Page 21 - 01

SLOSHING IN A T-BAFFLED RECTANGULAR STORAGE TANK 19
NUMERICAL STUDY FOR 2–D PROBLEMS

0.0036 1631
0.0033 2331
4631

P/gL P/gL0.003

0.0027

3 6 9 12 15 18

t

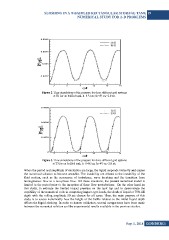
Figure 2. Time simulations of the pressure for three different grid systems
at T1 for un-baffled tank. h=0.31 m; θ0=40; ωR=2.0 r/s.

0.0009 1631
0.0006 2331
4631

0.0003

0
3 6 9 12 15 18

t

Figure 3. Time simulations of the pressure for three different grid systems
at T3 for un-baffled tank. h=0.465 m; θ0=40; ωR=2.0 r/s.

When the period and amplitude of excitation are large, the liquid responds violently and causes
the numerical solution to become unstable. The instability are related to the instability of the
fluid motion, such as the occurrence of turbulence, wave breaking and the transition from
homogeneous flow to a two-phase flow. For these situations, the present numerical model is
limited to the period prior to the inception of these flow perturbations. On the other hand, in
this study, to estimate the limited impact pressure on the tank top and to demonstrate the
capability of the numerical code in computing impact-type loads, the slosh of liquid at 75% fill
depth with the rolling amplitude 80 are chosen for all cases. Thus, the main purpose of this
study is to assess numerically how the height of the baffle relative to the initial liquid depth
affects the liquid sloshing. In order to denote validation, several comparisons have been made
between the numerical solution and the experimental results available in the previous studies.

Sayı 1, 2014 GiDB|DERGi